The Specter of Undefined Behavior
If you’ve ever spoken to a programmer, and really got them on a roll, they may have said the words “undefined behavior” to you. Since you speak English, you probably know what each of those words mean, and can imagine a reasonable meaning for them in that order. But then your programmer friends goes on about “null-pointer dereferencing” and “invariant violations” and you start thinking about cats or football or whatever because you are not a programmer.
I often find myself being asked what it is that I do. Since I’ve spent the last few years working on my Computer Science degree, and have spent much of that time involved in programming language research, I often find myself trying to explain this concept. Unfortunately, when put on the spot, I usually am only able to come up with the usual sort of explanation that programmers use among themselves: “If you invoke undefined behavior, anything can happen! Try to dereference a null pointer? Bam! Lions could emerge from your monitor and eat your family!” Strictly speaking, while I’m sure some compiler writer would implement this behavior if they could, it’s not a good explanation for a person who doesn’t already kind of understand the issues at play.
Today, I’d like to give an explanation of undefined behavior for a lay person. Using examples, I’ll give an intuitive understanding of what it is, and also why we tolerate it. Then I’ll talk about how we go about mitigating it.
Division By Zero
Here is one that most of us know. Tell me, what is 8 / 0? The answer of course is “division by zero is undefined.” In mathematics, there are two sorts of functions: total and partial. A total function is defined for all inputs. If you say a + b, this can be evaluated to some result no matter what you substitute for a and b. Addition is total. The same cannot be said for division. If you say a / b, this can be evaluated to some result no matter what you substitute for a and b unless you substitute b with 0. Division is not total.
If you go to the Wikipedia article for division by zero you’ll find some rationale for why division by zero is undefined. The short version is that if it were defined, then it could be mathematically proven that one equals two. This would of course imply that cats and dogs live in peace together and that pigs fly, and we can’t have that!

However, there is a way we can define division to be total that doesn’t have this issue. Instead of defining division to return a number, we could define division to return a set of numbers. You can think of a set as a collection of things. We write this as a list in curly braces. {this, is, a, set, of, words} I have two cats named Gatito and Moogle. I can have a set of cats by writing {Gatito, Moogle}. Sets can be empty; we call the empty set the null set and can write it as {} or using this symbol ∅. I’ll stick with empty braces because one of the things I hate about mathematics is everybody’s insistence on writing in Greek.
So here is our new total division function:
totalDivide(a, b)
if (b does not equal 0)
output {a / b}
otherwise
output {}
If you use totalDivide to do your division, then you will never have to worry about the undefined behavior of division! So why didn’t Aristotle (or Archimedes or Yoda or whoever invented division) define division like this in the first place? Because it’s super annoying to deal with these sets. None of the other arithmetic functions are defined to take sets, so we’d have to constantly test that the division result did not produce the empty set, and extract the result from the set. In other words: while our division is now total, we still need to treat division by zero as a special case. Let us try to evaluate 2/2 + 2/2 and totalDivide(2,2) + totalDivide(2,2):
1: 2/2 + 2/2
2: 1 + 1
3: 2
Even showing all my work, that took only 3 lines.
1: let {1} = totalDivide(2,2)
2: let {1} = totalDivide(2,2)
3: 1 + 1
4: 2
Since you can’t add two sets, I had to evaluate totalDivide out of line, and extract the values and add them separately. Even this required my human ability to look at the denominator and see that it wasn’t zero for both cases. In other words, making division total made it much more complicated to work with, and it didn’t actually buy us anything. It’s slower. It’s easier to mess up. It has no real value. As humans, it’s fairly easy for us to look at the denominator, see that it’s zero, and just say “undefined.”
Cartons of Eggs
I’m sure many of you have a carton of eggs in your fridge. Go get me the 17th egg from your carton of eggs. Some of you will be able to do this, and some of you will not. Maybe you only have a 12 egg carton. Maybe you only have 4 eggs in your 18 egg carton, and the 17th egg is one of the ones that are missing. Maybe you’re vegan.
A basic sort of construct in programming is called an “array.” Basically, this is a collection of the same sort of things packed together in a region of memory on your computer. You can think of a carton of eggs as an array of eggs. The carton only contains one sort of thing: an egg. The eggs are all packed together right next to each other with nothing in between. There is some finite amount of eggs.

If I told you “for each egg in the carton, take it out and crack it, and dump it in a bowl starting with the first egg”, you would be able to do this. If I told you “take the 7th egg and throw it at your neighbor’s house” you would be able to do this. In the first example, you would notice when you cracked the last egg. In the second example you would make sure that there was a 7th egg, and if there wasn’t you probably picked some other egg because your neighbor is probably a jerk who deserves to have his house egged. You did this unconsciously because you are a human who can react to dynamic situations. The computer can’t do this.
If you have some array that looks like this (array locations are separated by | bars | and * stars * are outside the array) ***|1|2|3|*** and you told the computer “for each location in the array, add 1 to the number, starting at the first location” it would set the first location to be 2, the second location to be 3, the third location to be 4. Then it would interpret the bits in the location of memory directly to the right of the third location as a number, and it would add 1 to this “number” thereby destroying the data in that location. It would do this forever because this is what you told the machine to do. Suppose that part of memory was involved in controlling the brakes in your 2010 era Toyota vehicle. This is obviously incredibly bad, so how do we prevent this?
The answer is that the programmer (hopefully) knows how big the array is and actually says “starting at location one, for the next 3 locations, add one to the number in the location”. But suppose the programmer messes up, and accidentally says “for the next 4 locations” and costs a multinational company billions of dollars? We could prevent this. There are programming languages that give us ways to prevent these situations. “High level” programming languages such as Java have built-in ways to tell how long an array is. They are also designed to prevent the programmer from telling the machine to write past the end of the array. In Java, the program will successfully write |2|3|4| and then it will crash, rather than corrupting the data outside of the array. This crash will be noticed in testing, and Toyota will save face. We also have “low level” programming languages such as C, which don’t do this. Why do we use low level programming languages? Let’s step through what these languages actually have the machine do for “starting at location one, for the next 3 locations, add one to the number in the location”: First the C program:
NOTE: location[some value] is shorthand for “the location identified by some value.” egg_carton[3] is the third egg in the carton. Additionally, you should read these as sequential instructions “first do this, then do that” Finally, these examples are greatly simplified for the purposes of this article.
1: counter = 1
2: location[counter] = 1 + 1
3: if (counter equals 3) terminate
4: counter = 2
5: location[counter] = 2 + 1
6: if (counter equals 3) terminate
7: counter = 3
8: location[count] = 3 + 1
9: if (counter equals 3) terminate
Very roughly speaking, this is what the computer does. The programmer will use a counter to keep track of their location in the array. After updating each location, they will test the counter to see if they should stop. If they keep going they will repeat this process until the stop condition is satisfied. The Java programmer would write mostly the same program, but the program that translates the Java code into machine code (called a compiler) will add some stuff:
1: counter = 1
2: if (counter greater than array length) crash
3: location[counter] = 1 + 1
4: if (counter equals 3) terminate
5: counter = 2
6: if (counter greater than array length) crash
7: location[counter] = 2 + 1
8: if (counter equals 3) terminate
9: counter = 3
10: if (counter greater than array length) crash
11: location[count] = 3 + 1
12: if (counter equals 3) terminate
As you can see, 3 extra lines were added. If you know for a fact that the array you are working with has a length that is greater than or equal to three, then this code is redundant.
For such a small array, this might not be a huge deal, but suppose the array was a billion elements. Suddenly an extra billion instructions were added. Your phone’s processor likely runs at 1-3 gigahertz, which means that it has an internal clock that ticks 1-3 billion times per second. The smallest amount of time that an instruction can take is one clock cycle, which means that in the best case scenario, the java program takes one entire second longer to complete. The fact of the matter is that “if (counter greater than array length) crash” definitely takes longer than one clock cycle to complete. For a game on your phone, this extra second may be acceptable. For the onboard computer in your car, it is definitely not. Imagine if your brakes took an extra second to engage after you push the pedal? Congressmen would get involved!

In Java, reading off the end of an array is defined. The language defines that if you attempt to do this, the program will crash (it actually does something similar but not the same, but this is outside the scope of this article). In order to enforce this definition, it inserts these extra instructions into the program that implement the functionality. In C, reading off the end of an array is undefined. Since C doesn’t care what happens when you read off the end of an array, it doesn’t add any code to your program. C assume you know what you’re doing, and have taken the necessary steps to ensure your program is correct. The result is that the C program is much faster than the Java program.
There are many such undefined behaviors in programming. For instance, your computer’s division function is partial just like the mathematical version. Java will test that the denominator isn’t zero, and crash if it is. C happily tells the machine to evaluate 8 / 0. Most processors will actually go into a failure state if you attempt to divide by zero, and most operating systems (such as Windows or Mac OSX) will crash your program to recover from the fault. However, there is no law that says this must happen. I could very well create a processor that sends lions to your house to punish you for trying to divide by zero. I could define x / 0 = 17. The C language committee would be perfectly fine with either solution; they just don’t care. This is why people often call languages such as C “unsafe.” This doesn’t mean that they are bad necessarily, just that their use requires caution. A chainsaw is unsafe, but it is a very powerful tool when used correctly. When used incorrectly, it will slice your face off.
What To Do
So, if defining every behavior is slow, but leaving it undefined is dangerous, what should we do? Well, the fact of the matter is that in most cases, the added overhead of adding these extra instructions is acceptable. In these cases, “safe” languages such as Java are preferred because they ensure program correctness. Some people will still write these sorts of programs in unsafe languages such as C (for instance, my own DMP Photobooth is implemented in C), but strictly speaking there are better options. This is part of the explanation for the phenomenon that “computers get faster every year, but [insert program] is just as slow as ever!” Since the performance of [insert program] we deemed to be “good enough”, this extra processing power is instead being devoted to program correctness. If you’ve ever used older versions of Windows, then you know that your programs not constantly crashing is a Good Thing.

This is fine and good for those programs, but what about the ones that cannot afford this luxury? These other programs fall into a few general categories, two of which we’ll call “real-time” and “big data.” These are buzzwords that you’ve likely heard before, “big data” programs are the programs that actually process one billion element arrays. An example of this sort of software would be software that is run by a financial company. Financial companies have billions of transactions per day, and these transactions need to post as quickly as possible. (suppose you deposit a check, you want those funds to be available as quickly as possible) These companies need all the speed they can get, and all those extra instructions dedicated to totality are holding up the show.
Meanwhile “real-time” applications have operations that absolutely must complete in a set amount of time. Suppose I’m flying a jet, and I push the button to raise a wing flap. That button triggers an operation in the program running on the flight computer, and if that operation doesn’t complete immediately (where “immediately” is some fixed, non-zero-but-really-small amount of time) then that program is not correct. In these cases, the programmer needs to have very precise control over what instructions are produced, and they need to make every instruction count. In these cases, redundant totality checks are a luxury that is not in the budget.
Real-time and big data programs need to be fast, so they are often implemented in unsafe languages, but that does not mean that invoking undefined behavior is OK. If a financial company sets your account balance to be check value / 0, you are not going to have a good day. If your car reads the braking strength from a location off to the right of the braking strength array, you are going to die. So, what do these sorts of programs do?
One very common method, often used in safety-critical software such as a car’s onboard computer is to employ strict coding standards. MISRA C is a set of guidelines for programming in C to help ensure program correctness. Such guidelines instruct the developer on how to program to avoid unsafe behavior. Enforcement of the guidelines is ensured by peer-review, software testing, and Static program analysis.
Static program analysis (or just static analysis) is the process of running a program on a codebase to check it for defects. For MISRA C, there exists tooling to ensure compliance with its guidelines. Static analysis can also be more general. Over the last year or so, I’ve been assisting with a research project at UCSD called Liquid Haskell. Simply put, Liquid Haskell provides the programmer with ways to specify requirements about the inputs and outputs of a piece of code. Liquid Haskell could ensure the correct usage of division by specifying a “precondition” that “the denominator must not equal zero.” (I believe that this actually comes for free if you use Liquid Haskell as part of its basic built-in checks) After specifying the precondition, the tool will check your codebase, find all uses of division, and ensure that you ensured that zero will never be used as the denominator.
It does this by determining where the denominator value came from. If the denominator is some literal (i.e. the number 7, and not some variable a that can take on multiple values), it will examine the literal and ensure it meets the precondition of division. If the number is an input to the current routine, it will ensure the routine has a precondition on that value that it not be zero. If the number is the output from some other routine, it verifies that the the routine that produced the value has, as a “postcondition”, that its result will never be zero. If the check passes for all usages of division, your use of division will be declared safe. If the check fails, it will tell you what usages were unsafe, and you will be able to fix it before your program goes live. The Haskell programming language is very safe to begin with, but a Haskell program verified by Liquid Haskell is practically Fort Knox!
The Human Factor
Humans are imperfect, we make mistakes. However, we make up for it in our ability to respond to dynamic situations. A human would never fail to grab the 259th egg from a 12 egg carton and crack it into a bowl; the human wouldn’t even try. The human can see that there is only 12 eggs without having to be told to do so, and will respond accordingly. Machines do not make mistakes, they do exactly what you tell them to, exactly how you told them to do it. If you tell the machine to grab the 259th egg and crack it into a bowl, it will reach it’s hand down, grab whatever is in the space 258 egg lengths to the right of the first egg, and smash it on the edge of a mixing bowl. You can only hope that nothing valuable was in that spot.
Most people don’t necessarily have a strong intuition for what “undefined behavior” is, but mathematicians and programmers everywhere fight this battle every day.
Object Oriented Haskell
You may recall, earlier this year I wrote about object orientation in C. The basic Idea being that “Object Oriented Programming” is more a mindset, then a language feature. You can do object orientation and access control in C using free-floating functions and opaque structs. Well, guess what? You can do Object Oriented Programming in Haskell as well!
As a quick recap, if you didn’t read "C With Classes", for our purposes there are three components that need to be present to be considered “an object”: data consolidation, access control, and method calling. Inheritance is also important to real “Object Oriented Programming” (or OOP, as I’ll start calling it), but is really just gravy. Inheritance is largely supported by typeclasses in Haskell, so I won’t be going into it today.
Functional OOP
What would OOP look like in Haskell? Thanks to the magic of higher-order functions, we can actually very closely approximate what you’d see in a traditional OOP language, such as Java or C++.
Data
This part is trivial, there is literally a data keyword for this purpose. You should have this down by now.
Access Control
Access Control can be accomplished by way of the module keyword. Simply expose what you’d like to be public, and don’t expose your private members. Obviously, if you have private fields in your “Class”, you should make a factory function for your class instead of exposing its constructor. This is all pretty standard stuff.
Method Calls
This is an area that Haskell shines, and C shows its ugly side. In Haskell, we can actually create a method call operator, and create something that looks very much like the traditional Class.method calling convention that we’re used to!
The Method Call Operator
First, we need some contrived classes. Let’s go with everybody’s favorite: the Employee!
data Employee = Employee {name :: String,
employeeId :: Integer,
title :: String}Nothing fancy or non-standard here. We created an Employee “Class” in the traditional Haskell way. Due to our use of record syntax, we already have three getters: name, employeeId, and title.
Let’s make another function, so that we can have a method that takes arguments:
isSeniorTo :: Employee
-> Employee
-> Bool
isSeniorTo s f = (employeeId s) > (employeeId f)There is something extremely important to note about this function: the last argument is the object, not the first as it was in “C With Classes”. The reason for this is to allow us to partially apply this function, this will be crucial.
Now, let’s give it a shot to make sure everything is working:
*ghci> let boss = newEmployee "Chris" 1 "Author"
*ghci> let notBoss = newEmployee "Geoffrey" 2 "Associate"
*ghci> name boss
"Chris"
*ghci> isSeniorTo notBoss boss
TrueAll looks well, we create two Employee objects. Since Chris‘s employee ID is lower than Geoffrey‘s, the isSeniorTo method returns True. But this is all very wonky still, let’s create that method call operator already!
(>-) :: a
-> (a -> b)
-> b
(>-) o f = f oSince . and -> are already spoken for, I’ve gone with >- for my method call operator. The method call operator takes an arbitrary type a, and a function that takes the same type a, and returns a type b. Finally a type b is returned. The definition of this function couldn’t be simpler: we call the function on the passed-in object! Let’s see this in action:
*ghci> notBoss >- title
"Associate"
*ghci> boss >- isSeniorTo notBoss
TrueThis is just about as elegant as it gets; using the method call operator we just defined, we call a method on an object! In the case of isSeniorTo, we partially apply the function with all but the last argument, then the method call operator is able to use it just as any other function.
But something doesn’t sit right. Isn’t the definition of isSeniorTo a bit smelly? It calls methods on objects, shouldn’t it use the method call operator? Now that we have our method call operator, let’s fix that function:
isSeniorTo :: Employee
-> Employee
-> Bool
isSeniorTo s f = (s >- employeeId) > (f >- employeeId)There, that’s better. isSeniorTo now properly calls methods on s and f, and all is again well in the world.
Here’s The Kicker
You may be experiencing some deja vu from all of this. It feels like we’ve done this sort of thing before. But where? You may recall this little operator:
*ghci> :t (>>=)
(>>=) :: Monad m => m a -> (a -> m b) -> m bThat’s right, the monadic bind operator looks suspiciously like our method call operator. But does it behave the same?
*ghci> 1 >- (+) 1
2
*ghci> Just 1 >>= (\a -> return $ a + 1)
Just 2Let’s ignore for a second that we had to use a monad for the bind operator, and see the fact that the two basically did the same thing. In fact, to further illustrate the point, let’s make a Class monad:
data Class a = Class a deriving (Show)
instance Monad Class where
(Class a) >>= f = f a
return = ClassUnlike most monads, which do important work, our Class monad does nothing but prove a point. However, you should note that the implementation of the bind operator is essentially the same as the implementation of the method call operator. Now, let’s see our monad in action!
let boss = Employee "Chris" 1 "Author"
*ghci> boss >- name
"Chris"
*ghci> Class boss >>= return . name
Class "Chris"As you can see, they essentially do the same thing. It turns out that Haskell had classes all along!
Of course, this isn’t exactly true. I’d say that the State monad serves many of the same purposes as objects in OOP languages. However, the semantics of things like Reader, Maybe, and IO have little in common with objects. But much like we implemented Objects in Haskell, the various OOP languages are implementing monads into their standard libraries.
Indeed, OOP and functional programming are not supported by languages, they are supported by programmers. Some languages may make one or the other easier, but the differences are small, and get smaller as time passes.
On ArrayLists and Vectors
Long ago, when I first started doing Java, I struggled against Java’s limitations regarding the resizing of arrays. Eventually after poking around for solutions, I found the ArrayList. Before that, I found the Vector, but for whatever reason, NetBeans was saying that Vector was deprecated, so I settled on ArrayList, and it was fine.
A few years later, I took my first class on C++, and learned about the std::vector. I was also introduced to the concepts of the vector and the linked list. Needless to say, I was confused. If vectors and linked lists aren’t the same thing, then what is this ArrayList thing? At the time, I elected not to pursue the question, needing to focus on figuring out these “pointer” things they were making us learn. I put it out of my mind.
Flash forward to today. This morning I was travelling the internet, and I came across a forum thread. The topic of the ArrayList came up. Curiosity finally overcame me, and I looked into the issue.
So, About Those ArrayLists…
The Java Collections framework is broken up into various datatype interfaces. There is an interface for lists, queues, maps, sets, and deqeues.
You’ll notice that there is no vector interface. While a list and an array have different semantics and use cases, you can use them roughly in the same way. “Array indexing” can be implemented on a list by iterating to the nth node, and arrays can be traversed like a list. Since there’s nothing a list can do that a vector can’t and vice versa, it follows that they can both implement the same interface. Sun had to make a choice: name that interface “list” or “vector”. They went with list.
Given that Java’s vector type implements the list interface, it follows that they would reflect that in the name: ArrayList. For all intents and purposes, ArrayList is equivalent to C++’s std::vector. ArrayList implements the Collections framework’s list interface, but it is a growable array. It behaves like a vector, indexing is cheap, resizing is expensive. Java also provides a LinkedList that behaves like a linked list.
So, what about Java’s Vector? It seems that Vector predates the Collections framework. After the introduction of the Collections framework Vector was retrofitted to be a part of it, also implementing the list interface. So, what’s the difference between ArrayList and Vector? Vector is synchronized, and therefore is safe to use in threaded code. Due to this it is significantly slower than ArrayList.
Simply put: use ArrayList in single-threaded code, and Vector in multi-threaded code.
Why Names Matter
This is why names matter. One might not think much of it, but imagine how many hiring managers would be out an interview question if ArrayList and Vector had been named Vector and SynchronizedVector respectively?
Happstack’s “Helpful” Exception Handler
Lately I’ve been messing around with web development in Haskell using Happstack. I believe that web development is something that a pure functional language excels in. Web apps are inherently stateless, so it stands to reason that a stateless programming language would be a good fit.
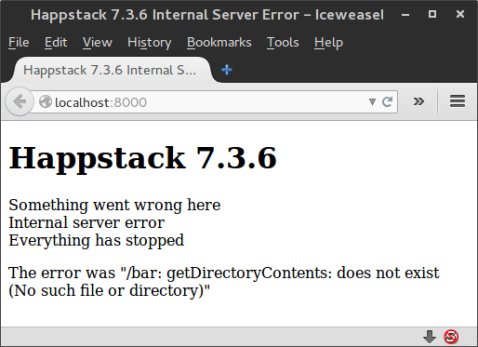
Happstack provides many of the nice features one would expect of a web framework. Among these things is a top-level exception handler to prevent exceptions from bringing down the server. Suppose you try to call head on an empty list:
willThrow :: ServerPart Response
willThrow = ok $ head []This will of course throw an exception. Happstack “helpfully” catches it and produces this output:
Why the air quotes? Notice how Happstack prints the exception message? While this might seem somewhat benign with a simple empty list exception (maybe even helpful if you’re troubleshooting), imagine you’re doing something a little less contrived:
maliciousThrow :: ServerPart Response
maliciousThrow = do dirs <- liftIO $ getDirectoryContents
"/bar"
ok $ toResponse $ show $ dirsOnce again Happstack airs out your dirty laundry.
In this case, it prints the fact that /bar doesn’t exist for the whole world to see. Great…
I spent some time searching around for the proper way to deal with exceptions in Happstack. There doesn’t seem to be much other than “handle them”. Personally, I feel that if an unhandled exception is thrown, Happstack should treat it as mzero.
This can be accomplished pretty simply:
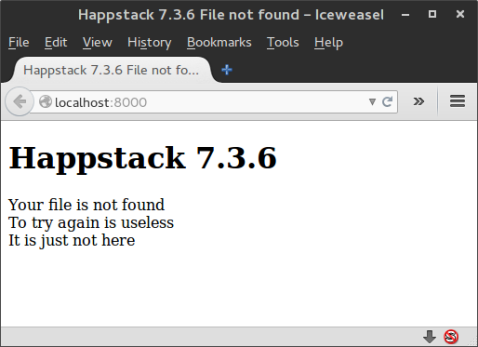
noThrow :: ServerPart Response
noThrow = do dirs <- liftIO $ tryGDC "/bar"
case (dirs) of Right d -> ok $ toResponse $ show $ d
Left _ -> mzero
where tryGDC :: String -> IO (Either SomeException [FilePath])
tryGDC a = try $ getDirectoryContents aThis function is similar to the previous maliciousThrow, except for the tryGDC function. This function uses the try function found within Control.Exception. Try attempts to perform some IO action, and returns Either an exception or a result, wrapped within an IO.
It is necessary to give tryGDC a function signature. Since functions can throw multiple exception types, the type checker cannot infer which is correct. In this case I’ve used the top-level exception class SomeException.
After trying, I check the result. On Right I return a ServerPart Response, on Left, I return mzero. Now when I attempt to access the page using this new version of maliciousThrow, I get this:
As it should be. It’s nobody’s business what went wrong.
Best Practices
It should be noted that the function noThrow is equivalent in quality to the following snippet of Java:
public static ThingDoer newThingDoer ()
{
try
{
return ThingDoerFactory.constructThingDoer();
}
catch (Exception ex)
{
return null;
}
}If you wrote that in a real application, you would be a Bad Person. Similarly, noThrow discards all info about what went wrong. You really should do something with it. Don’t show it to the user, but log it somewhere.
Update: I’ve posted a follow-up to this article, which can be found here!
DMP Photo Booth: Crunch Time
Over the last few months, I’ve become distracted. As anybody who’s ever committed to one project can probably tell you: it stops being exciting. What was once your pride and joy becomes the daily grind. Things get stale. As was the case with me, I suspect that this happens for most people when development of new features ends and the focus shifts to bug fixes.
I became distracted. My mind began to wander to the next thing, which in my case ended up being Haskell. I began learning Haskell, and it was definitely educational. I learned a lot with Haskell, and I plan to stick with it so that when I list it on my resume, I don’t get destroyed on a whiteboard test. Then came The Great Matrix Affair of 2014; I got overwhelmed at school. I spent so much time studying and doing homework that I couldn’t muster up the motivation to program. Things fell by the wayside, as you can see in my blog post output for February. Luckily for me, that is done, and I have the next two months free to program!
What Remains To Be Done?
It’s been a good 6 – 8 weeks since I’ve really focused on DMP Photo Booth, so the first order of business is the figure out what needs to get done. After doing some brainstorming I’ve settled on a list:
Finish The Trigger
I’ve mostly completed the trigger, but it doesn’t work. The button is soldered wrong, and while it was magically working for a while, it has since stopped. I need to fix the wiring issue, and then drill a hole in the box to put it through. After that and maybe a quick coat of paint it will be complete.
This particular task is due by Friday. I have a series of VIP demos coming up, the first of which is Saturday morning. A few of my cousins are coming in from out of town on Saturday to do wedding stuff, and I want to show it off then. While my cousin Allen is an engineer, and can appreciate a breadboard mockup of what will Totally Become A Real Thing, it certainly won’t be impressive. My cousin Laraine will likely be less amused, but I’m sure I’ll get a pat on the head for my “hard work”. Due to this, it’s important that the trigger be done before then.
Facebook Printer Module
The reference suite of modules was planned to be: a Trigger Module using my Arduino implementation, a Printer Module using CUPS, a Camera Module using LibGPhoto2, and a Lua module for each so that modules can be created using Lua. Of these, only the Lua Printer Module remains to be done. Since creating a Lua module is a trivial task (and not terribly important to be honest), this is a very low priority item.
However, the current Printer Module requires a physical printer. This might not always be ideal, since printers are big and heavy. What if you just want to bring a laptop and a camera and have a photo booth? My fiancée is having just this sort of situation; she wants to use the photo booth at her bachelorette party, but who wants to lug a huge printer to a hotel room? To solve this, I’ve promised her a Facebook Printer Module.
The idea is that when dmp_pm_print() is called, the photo strip will be uploaded to facebook. While I know this sort of thing can be done, I haven’t really researched it much. If it turns out that you have to pay facebook money to get this sort of access, I will find a hosting service that is free. Maybe Photobucket, or Dropbox, or whatever. The important thing is that the photo strips will end up in some central location on the internet so that anybody at the party can download the strip later. Ideally, this central location would be a facebook gallery so people can tag themselvs and be all Web 2.0.
My fiancée’s bachelorette party is in May, so this project isn’t a burning priority. However, this represents the most substantial addition of new functionality remaining to be done, so I plan to work it sooner rather than later. Code will be posted on my Github as it evolves, and like DMP Photo Booth will be available under the GPLv3.
Mac Support
To this point, all my development has been done in Linux. First using Ubuntu, and now using Debian. However, most people don’t use Linux. While Linux is the main target platform for DMP Photo Booth, I have been coding as portably as possible, so it should be little effort to port the application to Mac. Over the next few months, I’ll be making sure it compiles and runs correctly my old Macbook. My Macbook is vintage 2010, as such it is only running Snow Leopard. Therefore if anybody in the audience is a Mac user, and has a current version of OSX, feel free to give it a shot as well and let me know how it goes.
Ideally, my fiancée will bringing the Macbook to her bachelorette party and not my development laptop, therefore this project is due at the same time as the Facebook Printer Module, in May.
Bugs!
Finally, bugs. I need to identify them. I need to squash them. And I need unit tests.
After making a big show about being a good person and doing unit tests, I promptly lost the faith. Soon after implementing those first tests, I made a major change to how I handled errors in my code. Suddenly, all my tests were broken, and I was faced with the choice: rewrite them all, or delete them. After some thought I decided that my tests weren’t that great and that I’d probably change something again and break them all again. So I deleted them.
I’ve got to say, I miss those tests. There has been more than a few times where I’d refactored something and wasn’t sure if it still worked. Sure, it seems to work, but does it really? If I had unit tests in place, I could say with a greater degree of certainty that they do. Plus, “it sounds like a lot of work” is not a good reason not to do something, so it won’t be one for me.
On top of that, I’ll be identifying and squashing bugs the old fashioned way: by trying stuff. I’ve already found a few doozies, and I’m sure I’ll find more. As I find them I’m going to post them on the bug tracker for DMP Photo Booth on Github. I do this for a few reasons: 1) it will provide a public centralized repository of open issues so that I don’t lose or forget about them. 2) I would like others to post bugs here. If I post them here and show that I am fixing them, I feel it will establish confidence that it is looked at and acted upon.
This is due when DMP Photo Booth goes to version 1.0. That is planned to be on June 21, the day of my wedding. DMP Photo Booth will get a good solid night of work as the 80 or so people attending put it through its paces. Assuming all goes to plan with minimal issues, DMP Photo Booth will be declared to be out of Beta. That said, to be truly version 1.0, unit tests must be in place and “all bugs must be fixed”.
Packaging
Currently, DMP Photo Booth is available in source form only. No end-user ever had to compile Microsoft Office; I don’t feel they should have to compile DMP Photo Booth.
To that end, binary distributions will be available for Linux and Mac when DMP Photo Booth goes to version 1.0.
Got My Work Cut Out For Me
It’s a long list to be sure, but I have 4 months to focus on it. However, I’ve decided that I should spend some time focusing on other things too, so that I don’t burn out. To that end, I plan to spend 1 day per week focusing on learning new technologies, and 1 day per week keeping my old skills sharp.
For new technologies, this means things like learning more Haskell, and other languages or frameworks. Whatever strikes my fancy. For old skills this means practicing with Lua and Java, and maybe even C++ if I’m feeling particularly masochistic that day. This will likely take the form of blog posts on topics relating to these, so stay tuned!
Baby’s First Web Application Framework
Deep in the depths of the DMP Lunar Bunker, I have a file server running. I prefer to do my computing on various internet connected devices rather than be tied to one computer. To this end, I try to keep my documents, images, and things of that nature centralized on the server so that I can get to it anywhere. This is all fine and good on a computer, but my iPad and various smartphones don’t have native support for mounting a smb share.
To that end, a project that I’ve had planned for a long time is to develop a web app running on my server to serve that stuff up through a web browser. That said, this post isn’t announcing the beginning of that project. I have enough on my plate: DMP Photo Booth still needs polish, I want to learn Haskell, I have a wedding to plan, and I have to spend this month figuring out what “Linear Algebra” is. Not to mention that the file server is in need of a software refresh. All of those things are higher priority. That said, as an excercise in learning Haskell, I’ve created a toy HTML generator.
doopHtml
That would be the name of my little suite of functions. I feel its name reflects the gravity of the project. All that it really is is a few types, and customized show instances. First, let’s take a look at my types:
type TagName = String
type Attributes = [(String, String)]
data Child = NullChild |
TagChild Tag |
StringChild String
data Tag = NullTag |
Tag TagName Attributes [Child]First of all, forgive my sloppy indentation style. I haven’t really settled on a code style for Haskell yet. With that out of the way, let’s get to business.
TagName
This is just a type alias for a String. The concept of a math function is one that I understand, but I’ve always hated the trend of giving things useless names like a, i, or Σ instead of names like numerator, index, or Summation over. Sure, it was good enough for Aristotle, but I live in an age with things like “find and replace” and “code completion”. Maybe thousands of years from now, scholars will remember Chris Tetreault, father of the descriptive variable name. (HA!)
But I digress. I’ve created this alias to document when a String in a function argument or type constructor is a tag name.
Attributes
This is a type alias for an array of String pairs. This type represents the attributes list of a Tag. Things like src="http://doingmyprogramming.com/" It’s pretty self-explanatory. An empty list is an allowed value, and represents a tag with no attributes.
Child
Now we’re getting a bit more complicated. If you picture a HTML document as a tree, then the child is the branches from the top level tag. There are three types of Child: NullChild is the absence of a tag, TagChild is a nested Tag, StringChild is just some free floating text.
Tag
And now the meat of it. Tag has two type constructors: NullTag which is the absence of a tag, or Tag.
Tag takes 3 arguments: a TagName, an Attributes, and a list of Child. This is all you really need to represent a basic HTML document. (no embedded CSS)
None of these types have deriving(Show), because they require a custom implementation. Let’s look at that next.
Show
First, let’s take a look at Tag‘s Show implementation:
instance Show Tag where
show NullTag = ""
show (Tag n [] []) = "<" ++ n ++ ">"
show (Tag n a []) = "<" ++ n
++ flattenAttributes a ++ ">"
show (Tag n [] c) = show (Tag n [] [])
++ foldl1 (++) (map show c)
++ "</" ++ n ++ ">"
show (Tag n a c) = show (Tag n a [])
++ foldl1 (++) (map show c)
++ "</" ++ n ++ ">"The show tag has 5 patterns:
- The first pattern is a
NullTag. It returns an empty string. - The second pattern is a
Tagthat only has aTagName. It places theTagNamebetween angle brackets. - The third pattern is one that also has an
Attributes. It flattens theAttributes, and places it and theTagNamebetween angle brackets - The fourth pattern is one that has a
TagNameand aChildlist. It :- Recursively calls
showwith the argument(Tag n [] []). This results in the opening tag being printed mapsshowover theChildlist, then folds the returned list ofStrings up usingfoldl1 (++), concatenating all the returnedStrings into 1 largeString.- Closes the tag
- Recursively calls
- The fifth pattern has all fields. it works the same as the fourth, but calls the
show (Tag n a [])instead.
The Show implementation for Child is much simpler, and I don’t feel it requires explanation:
instance Show Child where
show NullChild = ""
show (TagChild x) = show x
show (StringChild x) = xBut what about that flattenAttributes function earlier? It looks like this:
flattenAttributes :: Attributes -> String
flattenAttributes [] = []
flattenAttributes x = foldl (\acc (k,v) -> acc ++ " " ++ k ++ "=" ++ v) "" xIf given an Empty List, it returns an Empty List. In Haskell, [] is the same thing as "", so this will function as an empty String. However, if not given an empty string the work is much more complicated.
First, foldl is called. foldl‘s function signature is: (a -> b -> a) -> a -> [b] -> a, which reads as: “foldl takes a function that takes an a, b, and returns an a. It also takes an a, and a list of b, and it returns an a”. In english, it needs a starting value, a list to fold up, and a function to be called on each list element. I call foldl on an empty string and x, which is the Attributes passed into the function.
The funky bit in the middle of all of that, (\acc (k,v) -> acc ++ " " ++ k ++ "=" ++ v), is called a Lambda. If you’ve ever written an anonymous function in Java, you’ve done this before. The \ at the beginning tells Haskell that what follows is a Lambda. After that, you have your arguments. Remember the signature of the function to be passed into foldl: (a -> b ->a). In this lambda, acc is a, and this is a String. (k,v) is b, a Tuple of two Strings. The part following the -> is the function body. In this lambda, we concatenate the two pairs together into the form of " k=v". That is then concatenated onto acc, which is the results of all previous calls. The final result looks something like " k1=v1 k2=v2 ... kn=vn", which is returned from the function.
Some Helpers
So, now that’s all done, and the Tag type is usable. It’s not user friendly though:
Tag "html" [] [TagChild $ Tag "head" [] [TagChild $ Tag "title" [] [StringChild $ "DMP"]], TagChild $ Tag "body" [] [TagChild $ Tag "a" [("href","doingmyprogramming.com")] [StringChild "Doing My Programming..."]]]
<html><head><title>DMP</title></head><body><a href=doingmyprogramming.com>Doing My Programming...</a></body></html>Barf, right? It’s like writing HTML, only harder! Clearly we need some helper functions to make working with this easier.
tagHtml :: [Child] -> Tag
tagHtml c = Tag "html" [] c
tagHead :: Attributes -> [Child] -> Tag
tagHead a c = Tag "head" a c
tagTitle :: String -> Tag
tagTitle t = Tag "title" [] [StringChild t]
tagBody :: Attributes -> [Child] -> Tag
tagBody a c = Tag "body" a c
pageSkeleton :: String -> [Child] -> Tag
pageSkeleton t b = tagHtml [TagChild $ tagHead [] [TagChild $ tagTitle t], TagChild $ tagBody [] b]Here is some basic helpers I whipped up while writing this. These four helpers will take just the fields needed to produce their respective tags. Now, we can make a basic page skeleton by calling the pageSkeleton function:
pageSkeleton "DMP" [TagChild $ Tag "a" [("href","http://doingmyprogramming.com")] [StringChild $ "Doing My Programming..."]]
<html><head><title>DMP</title></head><body><a href=doingmyprogramming.com>Doing My Programming...</a></body></html>While that could use some work, it’s enough to see where this is going. Much like Perl’s CGI module, functions can be created to automate much of the boilerplate.
Reinventing The Wheel
All this is fine and good, but surely this has been done already, right? Considering Haskell’s hackage server is implemented in Haskell, it seems that there is almost certainly a better web development framework for Haskell than doopHtml. I encourage you to not develop your next web application with the doopHtml framework, nor should you include your expertise in doopHtml on your resume.
It was good practice though!
Now For Something Completely Different
For as long as I’ve been trying (successfully or not) to program, I’ve been using C like languages. When I was a kid, I struggled in vain to learn C++. As an adult, I learned Java. After that, I used Java as a spring-board into the wonderful world of C Like Languages: C, C++, Perl, Lua. I wrote hello world in dozens of others as well. I found myself proudly proclaiming that “I’m confident I could pick up any C Like Language!”
Then one day I thought “what about the rest of them?” Sure, maybe I can speak Latin. Maybe I can pick up any Latin based language with relative ease. But what if I need to move to China? I speak C, but what if C falls out of favor for something else? I decided it was time to try something else.
But What?
C and it’s cousins broadly represent the Procedural and Object Oriented paradigms. We’ve all been there and done that. Procedures and Subroutines may or may not take arguments, do something, and may or may not return a result. The global or local state may or may not change. Loops happen. I don’t think it is a stretch to say that these are the two most mainstream paradigms. For the purposes of this blog post, I’m going to lump the Procedural and Imperative paradigms together. I understand that they are not the same thing, but roughly speaking, the Procedural paradigm is an evolution of the Imperative paradigm.
This leaves us with Functional Programming. Unlike the functions of an Object Oriented or Procedural language, the functions of a Functional language closely resemble those in math. In math, f(x+2), where x = 2, will always return 4. Similarly, a function in a Functional language will always return the same result given the same input. Where a function in a Procedural or Object Oriented language describes the steps to perform some task (usually, this involves some sort of loop construct), a function in a functional language just describes what the result of some function is. (usually involving recursion) f(x+f(x-1)) adds x to the result of f(x-1), which recursively adds x-1 to f(x'-1) and so on until the end of time.
So, what programming language to choose? Many languages support functional programming to an extent. Python, Lua, and even C# if you squint hard enough. However, these languages are multi-paradigm. As such, it will be easy to fall back into my C Like ways. What about Lisp?
Lisp is a family of languages: Common Lisp, Scheme, Clojure, Emacs Lisp. Sure, I could learn one, and theoretically be able to transition with ease, but this isn’t a level of fragmentation that I’m comfortable with. In addition, Lisps are multi-paradigm, so I’m more likely to not keep the faith. Which leaves me with…
Haskell
Haskell is a “pure” Functional programming language. While any useful program must have the side effect of reading from or writing to some external source, Haskell places that part of the program neatly in a corner. Let’s talk about some of the neat features of Haskell:
Lazy Evaluation
Expressions in Haskell are evaluated lazily. What this means is that a value isn’t computed until it’s needed. Let’s take a look at an example:
embiggen :: Int -> [Int]
embiggen x = x:embiggen (x + 1)This function takes an integer, and creates a list out of it. (Lists in Haskell behave much the same way as a normal linked list: O(1) insertion, O(n) traversal) The passed-in integer is pushed on to the front of the list resulting from embiggen (x + 1). You may have noticed that this function will go on forever. While maybe not ideal, this is ok in Haskell because of Lazy evaluation. The infinityeth element of this list will not be evaluated until it’s needed!
show (take 5 (embiggen 5))
[5,6,7,8,9]
show (embiggen 5) !! 17
22
show (embiggen 5)
[OMG INFINITE RECURSION!!!!!]In the first example, we call the library function take, which returns a list containing the first n elements of the passed in list. In the second example, we call the library function !! (all operators are functions), which is the list indexing operator, which returns the nth element of the list. In a language with strict evaluation, the list would need to be completely evaluated before these things could happen. In Haskell, it doesn’t! Only in the third example, where we attempt to call show on the entire list, does infinite recursion occur.
Tail Call Optimization
This is one of those terms that gets thrown around a lot, but what does it actually mean? The short answer is that it prevents a recursive function call from consuming a new stack frame. In a language without this feature, if foo() calls itself, the new call will consume a new stack frame. This will cause a stack overflow if allowed to go on too long. In Haskell, this isn’t a problem because of Tail Call Optimization.
Type System
Haskell’s type system is quite different from the usual type systems. Sure there are Ints, Chars, Floats, Bools, and the like, but there’s more to it than that. Haskell is very strongly typed. There is no casting in Haskell, if a function takes an Int, there’s no getting around giving it an Int. However, the whole type system operates in a manner similar to generics in languages like C++ or Java. Take the following examples:
putInList :: a -> [a]
putInList thing = [thing]
addStuff :: (Num a) => a -> a -> a
addStuff lhs rhs = lhs + rhsThe first function takes some arbitrary type, and returns a singleton list containing the passed-in argument. Much like generics, the argument shouldn’t depend on any type-specific behavior.
The second function takes two arguments of the same type that behaves like a number (Int, Float, Double, and friends) adds them, and returns the result. the addStuff function accomplishes this by specifying that arguments of type a should be members of the Num Typeclass. Despite the word “class”, Typeclasses aren’t the same as classes in Object Oriented languages. You CAN think of them as being the same as Java’s interfaces. When you create a type, you can make it a member of any number of Typeclasses. You must then implement the functions specified by the Typeclass, just like when a class in Java implements some interface, it must define the methods of that interface.
This is just the tip of the iceberg, but I’m sure you’re beginning to see how you can make very general functions in a very type-safe way.
Partial Function Application
A feature of functional programming is higher order functions. This means that functions can take functions as arguments, and functions can return functions. While nice, this isn’t exactly a new concept. Even C supports this to an extent with function pointers. What is new is partial application of functions. Recall the addStuff function above. It takes two arguments of type a and returns a result of type a. Now let’s look at an example:
doNumFunc :: (Num a) => (a -> a) -> a -> a
doNumFunc f a = f a
addThree :: (Num a) => a -> a
addThree a = addStuff 3 aThe doNumFunc function takes a function that takes a type a and returns a type a (This is what (a -> a) means), and a second type a, and returns a type a. doNumFunc calls the passed in function with the second passed in argument. The addThree function takes a type a and returns a type a. addThree takes an argument, and calls the addStuff function we defined earlier with its argument and 3. How does this all pan out?
addThree 3
6
doNumFunc addThree 3
6Seems pretty straightforward, right? Though, this isn’t very re-usable. What if I want to add 4? Do I need to define a function addFour? No, I can partially apply addStuff. If you call a function in Haskell with less arguments than it takes, it will return a function that takes the remaining arguments and returns a result! Observe:
doNumFunc (addStuff 3) 3
6Now things are getting cool. By calling (addStuff 3), we’ve created a function that takes a type a, adds 3 to it, and returns the result! You can’t do that in C!
Getting Started
Excited yet? You know you are, don’t try to act like you’re not. But how does one get started? Like any language, you need two things to begin: a compiler/interpreter and some reading material.
Environment
First up, you should go download the Haskell Platform. This package contains your compiler/interpreter and all the standard libraries. Haskell can be compiled, or interpreted. Or, you could use ghci, the interactive interpreter, if you just want to doop around and try stuff.
If you’re running a Linux distro, haskell-platform is likely in the repositories. In Debian or Ubuntu, it’s a simple:
sudo apt-get install haskell-platform… and you’re set! Unfortunately, there doesn’t seem to be a great IDE for Haskell. NetBeans definitely has nothing to offer in this regard. Luckily for us, Haskell is simple enough to not really need an IDE. GEdit, the default text editor that ships with Gnome, has built-in syntax highlighting for Haskell. Just enable the built-in terminal in GEdit to test stuff and you should be good to go. I like to run ghci in the embedded terminal to test functions as I write them. Plus, as you code, you can periodically attempt to load the script in ghci to make sure everything is formatted correctly and you haven’t messed up your syntax/types.
Literature
One of the biggest barriers to learning a new language is money. Nobody wants to put down cold hard cash on learning something new when what they have is working just fine. Luckily for us, you can learn you a Haskell for free! Learn You A Haskell For Great Good is a beginner’s guide to learning Haskell aimed at developers coming from C Like Languages. The best part is that the whole book is available to read online for free! You can check it out for the low-low price of zero dollars. If you like it, maybe you buy a copy for your bookshelf. Or maybe you just spread the word.
Whatever you do, you should have a good base of knowledge in Haskell. At that point, you can just consult Hoogle to learn more.
Last Train Out Of Cairo
After recovering from Christmas, and the terrible events of late 2013, it’s time to put my nose back to the grindstone with the printer module. My latest task: make the printer module not be terrible.
What’s so bad about the printer module, you ask? The short answer is all the things. All bad. Every single one of them. It’s slow. It doesn’t print right. It consumes way too much resources. It makes my cat sad.
The Brotherhood Of The Printer Developer
It all started when trying to figure out this whole printing thing. It turns out that printer development is one of those secret development clubs. There are no tutorials, the API documentation leaves something to be desired, and printing in Linux is bad in general. In short, it’d be easier to join the Illuminati than to infiltrate the Dark Cabal of Printer Developers.
Just by reading the CUPS API documentation, it’s not difficult to hash out a simple hello world type printer application. However, as anybody who has ever printed something knows, printing has lots of knobs to fiddle. However, the CUPS API does not seem to have functions corresponding to things like paper size and DPI.
During my research, I managed to turn up all of one StackOverflow post on the topic. The gist of it being “you set that up yourself using PostScript and send that to CUPS.” It also provides a sample implementation using Cairo.
Seems Reasonable
I decided to give it a shot. If nothing else, it would be a good introduction to the Cairo library for me. In my youth, I was fond of using Java’s Graphics2D library to make all sorts of fancy UI elements. In slightly oversimplified terms: Cairo is the GTK equivilent to Graphics2D. This isn’t entirely accurate: Cairo is a vector graphics library that GTK just happens to have adopted. Cairo is very usable outside the context of GTK; it can author a variety of file types including pdf and postscript.
I decided I’d use Cairo to author postscript within the printer module.
The Implementation
cairo_surface_t * base = cairo_ps_surface_create(
"[temp_file].ps",
[WIDTH],
[HEIGHT]);
cairo_surface_t * image =
cairo_image_surface_create_from_png(
"[photo_strip_filename]");First, I create 2 cairo_surface_t pointers. A Cairo surface is sort of like a canvas that you paint on. For those of you familiar with Java’s Graphics2D, you can think of it like your Graphics2D instance. cairo_surface_t is the base class of all Cairo surfaces, there are a variety of surface types for things like PostScript, PDF, PNG, X Windows, or whatever else. The first surface is an empty PostScript surface that represents our finished product. The second surface is created using our .png formatted photo strips.
cairo_t * working = cairo_create(base);If a cairo_surface_t is your canvas, then cairo_t is your brush. Think of it like a Java Stroke object. Right here, we are creating a new cairo_t from our base Cairo surface.
cairo_set_operator(working,
CAIRO_OPERATOR_DEST_OVER);
cairo_set_source_surface(working,
image, 0, 0);
cairo_paint(working);The basic idea is that you apply operations to a cairo_t, then you apply your cairo_t to a cairo_surface_t. Here, we are compositing our PNG surface over our PostScript surface. First we set the operator of our cairo_t to composite over the top. Next, we set the cairo_t to have our image Surface as its source surface. Finally, we call cairo_paint which will apply our cairo_t to the base surface.
cairo_surface_show_page(base);This call saves our PostScript file.
cairo_surface_destroy(base);
cairo_surface_destroy(image);
cairo_destroy(working);No C function is complete without a bunch of cleanup at the end. Here we call cairo_surface_destroy to free our cairo_surface_t pointers and then we call cairo_destroy to free our cairo_t pointer.
PS: You’re Doing It Wrong
That all seemed pretty great right? I thought so too. Here’s the problem: go check out that PostScript file you just created. Notice how it is 200 MB? Yeah…
It turns out that enormous PostScript files is a common problem. While we could just make sure to delete this file when we’re done, we’re still creating this gigantic file, then shoving it down our printer’s throat. My printer is on WiFi, so it takes a good 2 minutes to print this file, and brings my computer to a crawl while it’s doing it. No user is going to want to wait 2 minutes for their photo strip to print.
The second problem is actually a “feature” of PostScript. PostScript is a document layout language, and due to this the printer will take your PostScript file’s word for what it wants done. This sounds nice, until you realize that Cairo isn’t actually a PostScript authoring library. Cairo’s ability to tune a PostScript file is pretty limited. Specifically, this is a problem for things like DPI. I’m trying to print high quality images at 600 DPI. However, Cairo can’t set this in the PostScript, so the printer ends up spitting out a massively blown up copy of the image. This will not do…
The Solution
So, I’m back to square one. PostScript is a dead-end, and CUPS won’t let me customize my job. What to do…
I thought back to my hello world printer application. I was able to print a random image that was blown up to the size of my paper. What if I print an image that’s exactly the correct size for my paper? I gave it a shot, and sure enough there was no scaling issues!
I can set my printer to 600 DPI, then print my (600 * 4) x (600 * 6) image and it just works, just like Some Guy promised it would. All is once again well in the world.
Plus, I got some Cairo experience under my belt. Look forward to fancy curved lines and gradients in future versions of DMP Photo Booth! (Joking, I promise)
DMP Photo Booth: Deep Magick
After working on DMP Photo Booth for a few months, the day came when I needed to implement actual functionality. It’s the day we all dread, but for me this was no longer some looming menace; it was time to stop fiddling around in my framework and actually build on it.
More specifically, it was time to figure out how to turn ~5 images and a background into a photo strip. After checking to make sure GLib and GTK didn’t provide this functionality (GdkPixbuf almost cuts it, but as far as I can tell, it can’t layer images over each other), I turned to google. After some time, I settled on my library: ImageMagick.
ImageMagick bills itself as sort of a command-line PhotoShop. I was suspicious as well, but that’s neither here nor there. The thing about ImageMagick that interested me is its language bindings. ImageMagick provides a library for many languages, including two for C: MagickCore for “Wizard-level developers” and MagickWand for us chumps. Being a chump, I decided to go with MagickWand.
NetBeans configuration
This was relatively straightforward. If you got GTK set up, this should be no problem for you. First, ensure you have the WagickWand development headers. On Ubuntu, this can be accomplished by the following command:
sudo apt-get install libmagickwand5 libmagickwand-devOn my system, libmagickwand5 was already installed, so I downloaded the headers and got to work.
Next, in NetBeans click Tools->Options, click on the C/C++ tab, and click on Code Assistance. Add the location of the ImageMagick headers (/usr/include/ImageMagick for me). Click OK.
Next, we need to set up our project. Right click your project and click Properties. Click Build->C Compiler. Under Additional Options, add MagickWand to your pkg-config --cflags string. Click Build->Linker and do the same with your pkg-config --libs string.
You are now ready to conjure some magick!
Conjuring Some Magick
Now, let us put on our robes and wizard hats; it’s time to do some magick! Let’s go over a function that will overlay a resized image over a larger background. You can find the actual production photo strip function on Github.
void cast_magick_spell()
{
MagickWandGenesis();
...Before we can do anything, we must initialize MagickWand. “MagickWandGenesis()”, you ask? Of course the function would be called MagickWandGenesis, what kind of silly question is that?
...
MagickWand * background_wand = NewMagickWand();
MagickWand * working_wand = NewMagickWand();
MagickWand * final_wand = NULL;
...The MagickWand * is the main object passed around in a MagickWand application. Working with MagickWand requires some juggling of these pointers, which is why we have 3 of them.
...
if (!MagickReadImage(background_wand,
"/tmp/background.jpg")
{
...This function reads an image from a file. It returns MagickTrue on success, and MagickFalse on failure. If it returns MagickFalse, we have some clean-up to do…
...
ExceptionType exception_error_code;
char *
exception_message = MagickGetException(
background_wand,
&exception_error_code);
...MagickWand makes use of “Exceptions” throughout, so if a function fails, you can most likely pull an exception out of it using MagickGetException. Like any exception, it is up to you what to do with them. Since I’m using GLib, I’ve been wrapping them in a GError and propagating them up. This is actually very easy to do; your error code and message are already there. All you need to do is G_DEFINE_QUARK your error quark and throw it in there. For the purposes of this function, I’m just going to use printf, do some cleanup, and return.
...
printf("Oh no! Exception %d: %s\n",
exception_error_code,
exception_message);
MagickRelinquishMemory(exception_message);
DestroyMagickWand(background_wand);
DestroyMagickWand(working_wand);
return;
}
...Nothing particularly shocking here. We printf our message, free the exception_message string using MagickRelinquishMemory, free our MagickWands using DestroyMagickWand, and return.
Assuming we make it past this block, background_wand now contains the background image. Next, we load the foreground image:
...
if (!MagickReadImage(working_wand,
"/tmp/foreground.jpg")
{
/*
* Exception handling omitted
* for brevity. You should still
* do it here...
*/
}
if (!MagickResizeImage(working_wand,
[WIDTH],
[HEIGHT],
LanczosFilter,
[BLUR]));
{
/* More error checking... */
}
...After loading the foreground image, and doing our error checking we attempt to resize the image using MagickResizeImage. This function takes several parameters:
MagickWand * working_wand: The MagickWand to operate onsize_t [WIDTH]: the width to set the image tosize_t [HEIGHT]: the height to set the image toFilterTypes LanczosFilter: the filter to use to resize. There are a list of them in the API documentation. Discussion of these is outside the scope of this post.double [BLUR]: The blur factor to apply. 1.0 is no change. The further 1.0, the blurrier the resulting image.
Like many calls in this library, this function can return MagickTrue or MagickFalse. If it returns MagickFalse, something threw… Next, we adjust the position of the image…
...
if (!MagickResetImagePage(working_wand,
[RELATIVE_PAGE_SPECIFIER]))
{
/*
* You'd think one of these wizards
* could have written a function that
* doesn't throw...
*/
}
...This function takes some explaining. The second parameter: char * [RELATIVE_PAGE_SPECIFIER] is what’s doing the work here. This is a Magickally formatted string that looks like this: "100x100+15+15!". Let’s examine this as a printf formatting string:
"%dx%d+%d+%d!"
We have 4 integer tokens here. The first token is canvas width, and the second is the canvas height. Note that these will not resize the image, so don’t get any bright ideas about eliminating the previous resize call. The third and fourth tokens are offset from X and Y respectively. These are what we’re really concerned about here. This will allow us to position our foreground image over the background.
Also, don’t forget to check for exceptions!
...
MagickSetLastIterator(background_wand);
if (!MagickAddImage(background_wand,
working_wand))
{
/* exceptional! */
}
...We’re almost there! Now we have to add the images from working_wand to background_wand. These MagickWand objects are lists of images. Like most lists, they have iterators. The call to MagickSetLastIterator sets background_wand’s iterator to the last image in the list. Any images add will be added after this image. next we call MagickAddImage which adds copies of working_wand’s images into background_wand. As before, don’t forget to check for exceptions.
...
final_wand=MagickCoalesceImages(background_wand);
if (!final_wand)
{
/* You guessed it! */
}
MagickSetLastIterator(final_wand);
...Now we need to combine all our images into one single image. This is accomplished by calling MagickCoalesceImages which returns a new MagickWand with all of our images combined into 1. The MagickWand used for this call remains unaffected. Obviously, if final_wand == NULL, something threw.
After this is done, we need to set the iterator of final_wand to the Last Iterator, or the next step doesn’t work as advertised…
...
if (!MagickWriteImage(final_wand,
"/tmp/final.jpg"))
{
/* wait for it! */
}
...Shockingly, this function writes your new image to a file. Make sure you check your exceptions.
...
DestroyMagickWand(background_wand);
DestroyMagickWand(working_wand);
DestroyMagickWand(final_wand);
MagickWandTerminus();
}…and were done! Clean up your pointers and call MagickWandTerminus to finalize the MagickWand library. If you browse to /tmp, you should have a newly created final.jpg if all was well!
Would I Do It Again?
Sure.
ImageMagick was a decently easy to work with library. The documentation wasn’t amazing, but it was tolerable. I’m still a little hazy on the use of the [RELATIVE_PAGE_SPECIFIER], but it’s working so far. One nice thing about the docs is that there are many examples. If the docs don’t explain something, you can look up an example and get an idea of how things work.
The only really big issue I have with this library is how it handles exceptions. This is an issue that I’ve touched on before; it is all too easy to forget to check a return code. I went down that road with DMP Photo Booth, and I’ve since rejected it. I spent an entire day refactoring my program to use GError.
MagickWand has exceptions, they’re just really easy to ignore. While writing this blog post, I caught several instances of unchecked return values in my 1 function that uses MagickWand. Tomorrow I plan to fix this, but it’s time I could be spending on something else.
If GError is Java’s checked exceptions with all it’s order and verbosity, then MagickWand’s exceptions are the Wild Wild West of C++’s unchecked exceptions. If you’ve spent any time working with C++, this has almost certainly bit you; some function doesn’t document if it throws, and your program magickally starts crashing because you didn’t catch something. Bad times are had by all. Sure, you could throw a try/catch block in main() and catch all exceptions to keep from crashing, but at that point your program is a dead man walking. Best to put it out of its misery…
Personally, if I ever write a personal project in C++ again, I’m likely to disable exceptions in my program; they’re just more effort than they’re worth. Maybe I’d even use GError in my C++ app if I could convince myself that I’m not a bad person for using a C library in C++.
Regardless, one blemish on an otherwise pleasant experience is no big deal. Here’s to a successful foray into the land of High Adventure!
DMP Photo Booth: Throw It All Out
Another week goes by, another major refactor. This time on the chopping block: return codes. As you may know if you’ve been following development, I’ve been using integer return values to indicate success and failure of functions. This was working for a while, but as we all know, the worst problems don’t rear their ugly heads until some time has gone by. After working around them, I’ve realized this strategy has 3 main issues:
- It’s really easy to just not check the return value, and not notice when some function returns DMP_PB_OMG_WERE_ALL_GONNA_DIE
- It can be problematic if you have to return an integer as an actual result
- You have to settle on some “failure” return value for functions that return values, and this can be a problem if you can’t guarantee some value will never be valid
Too bad I didn’t pick a modern language with exception handling…
GError To The Rescue
Luckily for me, GLib has the answer once again. GLib has a feature called GError, that is its answer to exception handling. I’d tell you all about how to use GError, but there is no need. GLib’s documentation is on par with Java’s documentation, and the GError documentation page is a shining example of how good documentation can make the difference between good and great.
Seriously, if anybody from Gnome is reading this: thank you for writing some decent documentation. This is a huge pet peeve of mine. No, your function called do_stuff(some_struct * zanzibar) is not self documenting, because if you don’t write a comment telling me if it has side effects, or if I remain responsible for zanzibar, then I have to look at your code to be sure. But I digress…
The basic idea behind GError is that any function that can throw has a GError ** as its final argument. If you’d like to call a function that can throw, you need to pass in an unallocated pointer to the function:
void some_func()
{
GError * error = NULL;
dangerous_func(&error);
...At this point, dangerous_func will be called, and return. Afterwards, if your GError pointer is no longer NULL, then an exception was thrown:
if (error != NULL)
{
//what now?
}This test is equivalent to a catch {} block. At this point, you traditionally have 3 options: Handle the exception, re-throw the exception, or wrap the exception in some other exception type and throw.
Personally, I’m a huge fan of Java’s checked exceptions. Sure, it can be annoying having to catch 15 different exceptions because some library author thought they needed that many on one method, but it sure beats having to magically know if some function throws, as C++ handles things. I feel that GError strikes a good balance. If a function has a GError ** argument, then it throws. At this point, you can check the docs to see if the author felt fit to say what GErrors they set, or you can just read the error and see what it is. You don’t have to catch some specific Exception class as in traditional exception handling, and you can determine exception type without resorting to instanceof.
Now, let’s examine our options…
Handle It
if (error != NULL)
{
printf("%s %d: %s\n",
g_quark_to_string(error->domain),
error->code, error->message);
g_error_free(error);
}A GError has 3 public fields: domain, code, and message. Domain is a GQuark that is [NAMESPACE]_[MODULE]_ERROR. Think of this as your exception base class: i.e. BaseBeanFactoryBeanException. Code is an integer that represents a specific error. Think of this as your derived exception class: i.e. FluffyPinkBeanFactoryBeanException Finally, we have message. This is a human readable message for the error, and is equivalent to a Java call to Exception.getMessage().
GError has a few methods to ease working with these, but any C programmer worth their salt should be able to “make do” with these 3 fields.
Re-throw It
if (error != NULL)
{
g_propagate_error(this_funcs_gerror, error);
return;
}Yes, it is that simple. Of course, in this case, the function signature would be:
void some_func(GError ** this_funcs_gerror)…but aside from that, there’s not much going on here. The GError will be copied into the passed-in GError **. At this point you can (must) return; the error is now the caller’s problem!
Wrap It
if (error != NULL)
{
g_set_error(this_funcs_gerror, error->domain,
error->code,
"I know better, so I'm wrapping this!\n");
g_error_free(error);
return;
}Pretty self-explanatory. As with re-throwing the exception, this requires a modified function signature. Also, this is how you’d throw a new exception as well, minus the call to g_error_free.
The Empty Catch Block
We’re all guilty of this, don’t try to act like you’re not. It’s just so much easier to do this:
try
{
fancyObj.someDangerousMethod();
}
catch (Exception ex)
{}Don’t worry, you’re among friends. GLib has you covered on this front as well. If you pass NULL to a function that throws, it will not attempt to set an error, and you can just go on with your life:
void some_func()
{
dangerous_func(NULL);
//catch (Exception ex) {}
}Feel free to omit that comment, I promise it’ll still work. As we all know, sometimes you just don’t care about some exception. In these cases, you aren’t forced to care, you can just pass NULL and get on with your life.